One of the most common forms of magnetic components is inductance, which has a certain inductance value and therefore its impedance increases with the increase of frequency. This alone can be considered as a first-order high-frequency filter; When the filtering object we are discussing changes from a single current path (loop or circuit loop) to two or more, it is necessary to place at least one inductor on each path to achieve the same high-frequency filtering effect - this can be easily and cleverly designed in practical magnetic components, which is the common mode choke we are talking about here. Why? Because when there are multiple paths (such as the most common two), the magnetic flux generated by the same direction current can be "shared" with another current path, making it equivalent to obtaining additional impedance, also known as (magnetic) coupling. Thus, by winding two mutually coupled coil windings around a magnetic core, a better filtering effect can be achieved than using two separate inductors.

The above introduces the basic functional characteristics of common mode inductors, namely filtering. So, first of all, it is necessary to distinguish between transformers and common mode inductors that also require coupling operation, because filtering suppresses (or absorbs) noise on the line. From the excitation direction, it is common mode, but transformers transmit voltage excitation current representing power, which is differential mode. Therefore, similar to the connection of safety capacitors, common mode inductors need to be in the Y connection (through the ground circuit or reference ground circuit), while transformers need to be in the X connection (across the input and output circuits). Secondly, the evaluation and measurement of its common mode filtering effect itself require the use of additional auxiliary circuits. However, in actual EMC (Electromagnetic Compatibility) testing, it often only tests the receiver (LISN - Linear Impedance Stabilization Network) signal caused by the combination of differential mode and common mode to determine whether it complies with the corresponding regulatory standards (such as CE certification). Therefore, the role of common mode inductance is often difficult to find an answer in the specification book, which is also the reason why engineers often rely on experience to make simulation predictions when selecting models. Finally, observant readers will find that common mode inductors are called inductors, but they are not different from power inductors. They do not consider saturation current or energy storage, and their English names end in choke. Therefore, their basic meaning is still choke. As we will discuss later, it is precisely because of their choke effect that they can achieve filtering, so calling them common mode choke coils is more in line with their principle.

In the following section, we will learn about the basic structural principles, application classifications, and related selection of common mode inductors, hoping to be helpful to you as an engineer. Meanwhile, if you have any questions or wish to discuss the relevant introduction, please contact us. Our engineering team will provide you with as much assistance as possible from the perspective of components and applications.

一、Magnetic Field Coupling

As shown in Fig.1, the energized coil A will distribute a magnetic field in space near its current circuit (here the coil), represented by the magnetic flux Фa (or→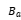) the application classification and selection of magnetic flux density common mode inductance. The strength of the magnetic field depends on the magnitude of the current, the number of turns of the coil, the effective cross-sectional area, and whether there is a magnetic core. The magnetic flux at the center of the coil can be approximately expressed as:

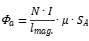
Among them, if there is a magnetic core at the center of the coil, its magnetic permeability 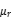 the larger it is, the corresponding equivalent magnetic circuit length  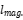the shorter it is, the greater the magnetic flux will inevitably be. This is a standard inductance structure and its corresponding spatial magnetic flux distribution. It is worth noting that its magnetic flux distribution does not depend on changes in current and is an identity relationship. Its essence is derived from the Gaussian magnetic field law in Maxwell's electromagnetic equations.

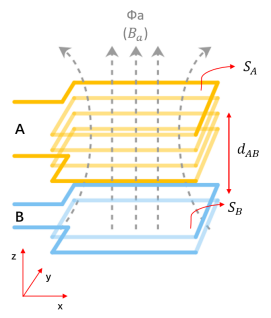
Fig.1 The spatial magnetic field distribution of energized coils A and B

When another coil B in space approaches the energized coil A in a certain positional relationship (as shown in Fig.1), the magnetic flux partially distributed by coil A will inevitably pass through coil B, forming a shared relationship. According to Ampere's Law, when the magnetic flux in the loop surrounded by coil B changes, an induced electromotive force, or induced voltage, will be generated in the loop of coil B. It can be foreseen that if coil B is an open conductive coil, no loop current can be formed, but only induced voltage is formed at both ends of coil B. Since there is no current on its loop, no corresponding spatial magnetic field will naturally be generated; However, if coil B is a closed loop, there will definitely be a loop current generated, that is, induced current. At the same time, since there is induced current, it will form a spatial magnetic field distribution in reverse. According to the spatial relationship between coil B and coil A, coil A will inevitably share the distributed magnetic flux of coil B. So, what will be the final result of such mutual induction? Obviously, if coil A only has a constant current, coil B will not feel any change in the magnetic flux it shares at a fixed position. Therefore, only when a changing current (such as alternating current) is generated in coil A can mutual induction occur. In a one-to-one situation (only looking at the situation where one coil is paired with another coil), the induced current always has an effect on counteracting the change in magnetic flux. Therefore, the corresponding coil B's influence on coil A will just cancel out the magnetic flux change shared by coil A to coil B. The magnetic flux shared by the two will cancel each other out in terms of change.

Magnetic field coupling in a fixed position (different from electric motors or generators) describes the interaction between different coils due to shared magnetic flux under alternating current conditions. As a transformer for power conversion or signal isolation, or as a common mode inductor for current compensation, it is a case of magnetic field coupling. When designing or producing a common mode inductor, it is always inevitable to consider a question: what parameters must the two coils ensure to meet the requirements? Or, besides current and one-sided inductance, what are the necessary requirements to consider the relationship between the two? A common parameter requirement is that the sensing error on both sides must be sufficiently small, or sometimes the coupling coefficient must reach a high level (such as>98%). This is because as a current compensation type common mode inductor, if the leakage inductance is too large, it will have a significant effect on the differential mode signal, either causing unnecessary differential mode impedance (resulting in signal attenuation or reduced differential mode bandwidth), or causing magnetic core saturation and affecting common mode noise suppression. Therefore, it is necessary to control the coupling coefficient of magnetic field coupling.

When magnetic field coupling occurs between two coils through a coupling medium (magnetic core) with uniform magnetic permeability, the specified magnetic flux shared by coil A to coil B is 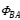 ，On the contrary, it is equaled to  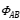. Then, because the shared magnetic flux (magnetic field coupling) corresponds to mutual inductance, it can be defined as the application classification and selection of common mode inductance and the application classification and selection of common mode inductance, respectively  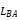and  : 

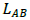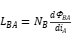
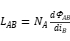
The total shared magnetic flux at the induction coil end is also known as linkage (linkage,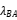), which can be represented by the relationship  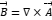between the based on magnetic flux density  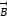and magnetic vector  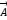position :

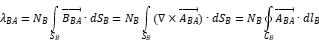
The magnetic vector position distributed by coil A at each point on coil B is (in the average case of application classification and selection with a center to center distance 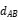 of common mode inductance) :

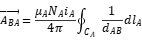
The flux linkage between coil A and coil B is obtained as follows:

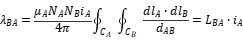
Therefore, the mutual inductance 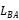 acting on coil A by coil B are as follows:

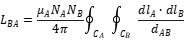
The same principle can be applied to obtain 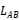 the expression for the:

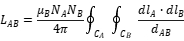
As mentioned earlier, magnetic field coupling occurs between two coils through a coupling medium (magnetic core) with uniform magnetic permeability. Therefore 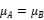, obviously:

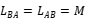
The above explanation states that two coils wound on the same magnetic core have the same mutual inductance, represented by M. The detailed proof process above can refer to Neumann's formula. Now, assuming that the total magnetic flux 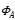of coil A the shared part 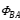the proportion of 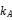, that is 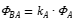. Similarly, the sharing coefficient of coil B is the 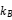, there will be:

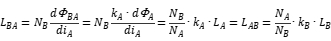
Therefore, the relationship between the mutual inductance between two coils and their independent inductance can be obtained from the above equation relationship:

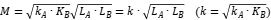
The above is the origin of the magnetic field coupling coefficient k: the actual common mode inductance can be determined by measuring the inductance values of two coil windings separately (the other coil remains in an open state), as well as the leakage inductance (the other coil remains in a closed state, 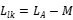), and the corresponding values of mutual inductance and coupling coefficient k. Specifically, for a very symmetrical common mode inductor wound on a high permeability annular magnetic core (such as a MnZn Ferrite magnetic ring), the inductance values of the two windings are very close, and the magnitude of the leakage inductance will be close to 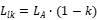. It can be seen that the higher the coupling coefficient, the lower the leakage inductance.

二、Application of Common Mode Inductors

As mentioned at the beginning of this article, a common mode inductor is nothing more than an inductor that is simultaneously connected across two current circuits. Its function is to suppress or attenuate common mode noise that may exist on both current circuits. However, these two parallel current circuits are not limited to the case of forming a differential circuit, such as the L and N lines in a pair of power lines, or the D+ and D- lines on the data line port. Due to the generation of common mode noise, common mode noise suppression may be required between transmission lines that share the same ground.

In order to determine the application of common mode inductance, it is first necessary to understand how common mode noise occurs: as shown in Fig.2 (reference design for Infineon's 60W switching power supply: DEMO_5QSAG_60W1), the input terminal is the mains input of 85~300VAC, and the wiring L, N on the power port forms a common ground with the reference ground. In fact, there is also a ground wire Green Line connected to this reference ground and connected to the physical ground. Now the L line and N line form the power circuit and are connected across the primary side of this Flyback transformer. The specification of Q11 as the main power switch tube uses the 800V super junction MOS transistor IPA80R600P7, with a maximum Rds (on) limit of 600m Ω. In order to limit heat dissipation, the heat dissipation medium (aluminum heat dissipation fins) is usually attached to its shell, which increases the stray capacitance of its high voltage pin to ground, forms capacitive coupling, and couples the high voltage and high frequency input terminal voltage to form a potential with noise properties. The L line and N line at the input port will also receive this potential through the reference ground, thus forming a common mode noise source. It is worth noting that capacitive coupling, as the main common mode noise source that conduction testing in EMC testing needs to face, widely exists in various power sources with AC-DC as the main form and different topology structures. At the same time, there are actually many small current circuits on the primary and secondary sides of transformers, and each small current circuit also increases the noise current of inductive coupling, which also brings difficult to predict common mode noise or differential mode noise. Therefore, it brings a lot of uncertainty to EMC rectification, which is also the reason why it is still impossible to rely on simulation software for electromagnetic compatibility simulation.

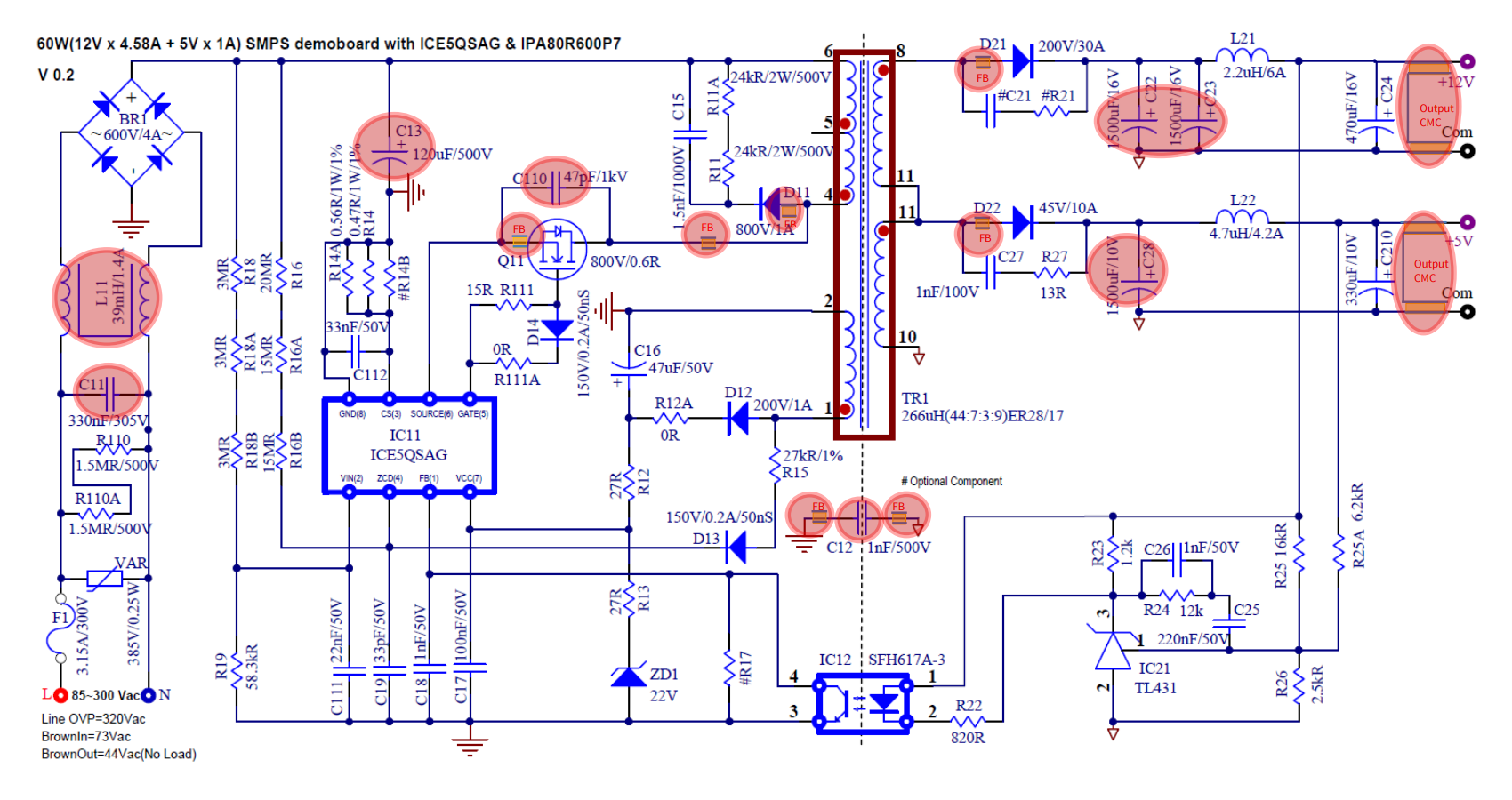
Fig.2 Example of EMI Corresponding Strategy Components (Infineon DEMO_5QSAG_60W1)

To estimate the magnitude of common mode noise, it is usually necessary to assume the stray capacitance on the common mode noise circuit, which is typically in the range of tens of pF. In the example shown in Fig.2, assuming a stray capacitance of 20pF, when the input power supply is 230Vac and the switching frequency of the main power switch tube is 200KHz, the total pulse width for turning on and off is 1µs and the rising and falling edges are 0.2µs, respectively. The maximum voltage at the input terminal is 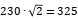V, the duty cycle of the AC input through the switch is 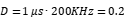. The first corner frequency in the spectral density distribution is:

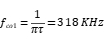
The corresponding voltage at the first peak (1st harmonic 1st harmonic) in the spectral density distribution is:

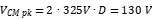
On a circuit with common mode noise, without connecting a common mode inductor, the maximum common mode current can be estimated by ignoring the series equivalent impedance (such as wire resistance, parasitic inductance, etc.), as shown in Fig.3. When connected to a LISN (linear impedance stabilization network), the magnitude of the common mode current is:

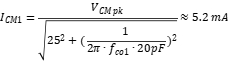
Therefore, the common mode noise voltage amplitude received by the conduction test receiver (spectrum analyzer) on the LISN port will be:

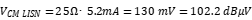
Although the actual result detected on the test receiver is:

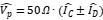
That is to say, the amplitudes of common mode noise and differential mode noise are superimposed, but obviously as long as the common mode is suppressed, the final test results will be improved. Therefore, for example, in the EMC standard EN55022 for conventional communication and industrial applications, the amplitude QP must be lower than 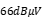 in the range of 150KHz to 500KHz. Therefore, the maximum  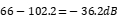attenuation of common mode noise must be carried out here. Taking the attenuation target of -20dB as an example, through simple calculation, the main impedance in the common mode circuit is the impedance of stray capacitance, which is approximately 25K Ω. As shown in Fig.4, the corresponding required common mode impedance is approximately 250K Ω, which can be converted into a 125mH common mode inductor.

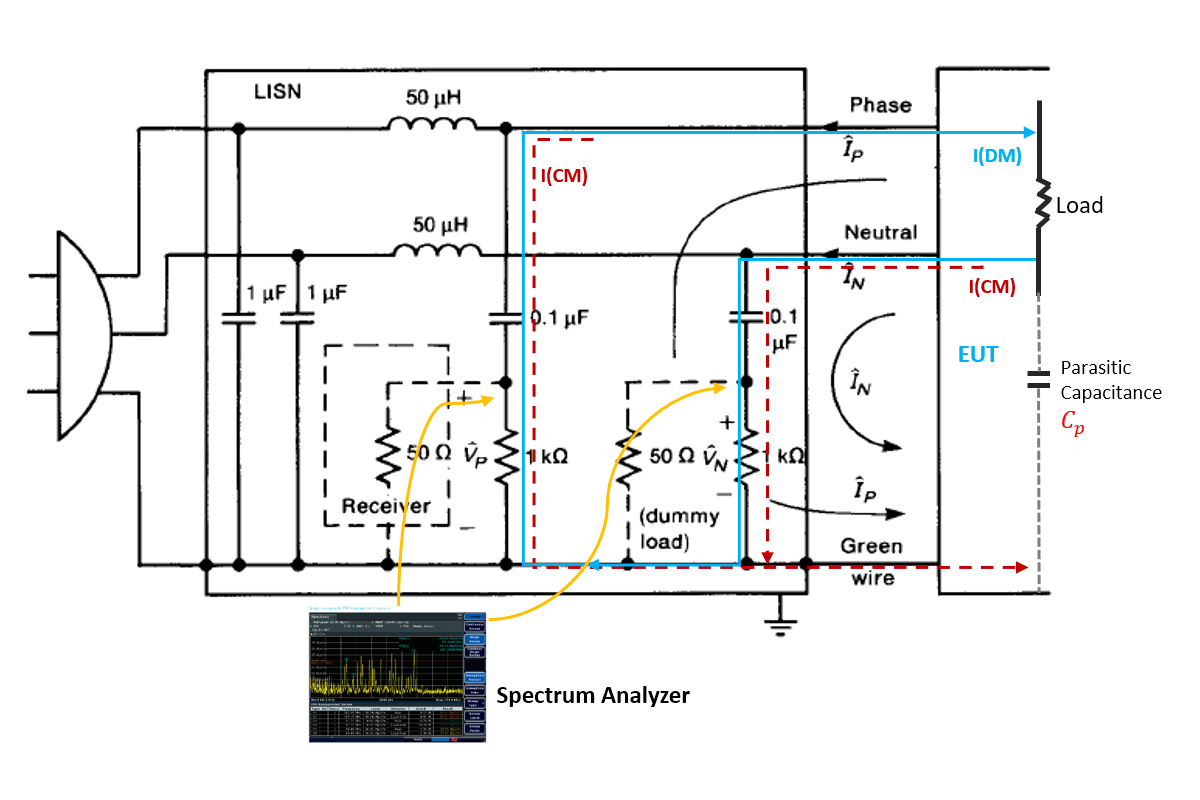
Fig.3 Schematic diagram of conduction test in EMC testing (circuit diagram of common mode noise and differential mode signal)

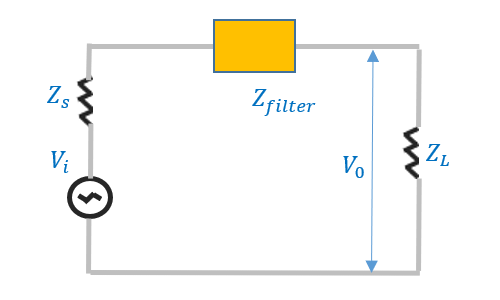
Fig.4 The relationship between the circuit of filter insertion loss (left) and the corresponding attenuation amplitude and filter impedance (right)

In addition to common mode inductance applications on power lines, common mode inductance is also commonly found on high-speed signal lines, such as USB 3.0, HDMI, LAN, etc., or some LVDS signal lines such as CAN BUS, SPI or RS232, RS485, etc. The use of common mode inductors on signal lines also has the function of suppressing common mode noise, such as the common mode rejection ratio required to meet certain communication specifications. However, the more important point comes from its accompanying current compensation effect, as mentioned at the beginning, which is the current compensation type common mode inductor.

As shown in Fig.5, high-speed signal lines generally use differential transmission to transmit signals. There are resistors, stray capacitors, and distributed inductors on the signal lines. Twisted pair cables can effectively reduce stray capacitors but cannot remove distributed inductors. Therefore, there is differential input inductance at the receiving end, and the coupling current on the line will form noise on the signal diagram. These noises are distributed almost equally at both ends of the receiver based on the symmetry of the transmission line. Now that a common mode inductor is placed at the input position of the receiver, the almost equal amount of noise will be cancelled out through the winding coupling of the common mode inductor, greatly reducing the coupling noise. That is, the current compensation effect reduces the input noise at the receiver.

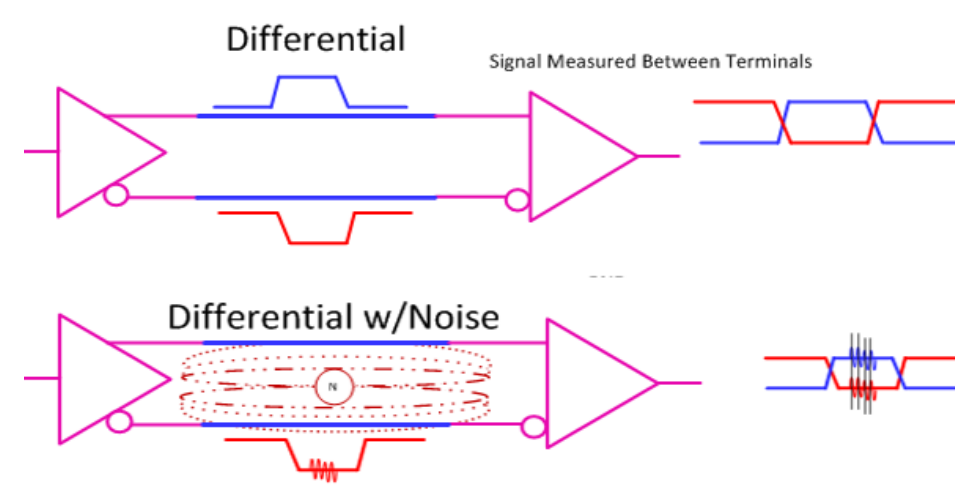
Fig.5 The transmission process of differential signals along the transmission line from the transmitting end to the receiving end (left) and the improvement of using common mode inductors at the receiving end (right)

On the eye diagram of the signal, as shown in Fig.6, by reducing the insertion loss caused by line stray inductance, the signal-to-noise ratio will be improved, which is important for longer transmission lines or high-speed signal lines. Generally speaking, the transmission lines used for the signal ports mentioned above are usually 90~120 Ω impedance transmission lines. Based on specific signal bandwidth requirements, impedance common mode inductors ranging from 1 to 10 times are generally selected to provide -6dB to -20dB common mode suppression. This is similar to the power supply application mentioned earlier, depending on the impedance size of the common mode noise circuit. Of course, as the frequency increases (due to the requirements of high-speed signal transmission), the common mode impedance of the system will decrease, and providing excessive inductance will narrow the filtering bandwidth. Therefore, it is necessary to verify whether the selected inductance matches the transmission requirements of high-speed signals.

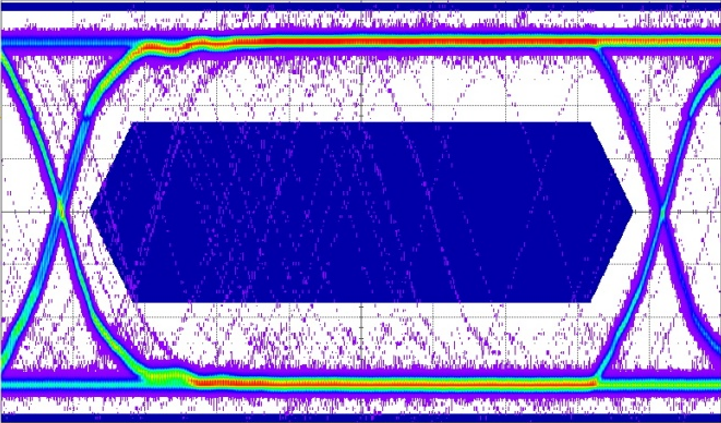
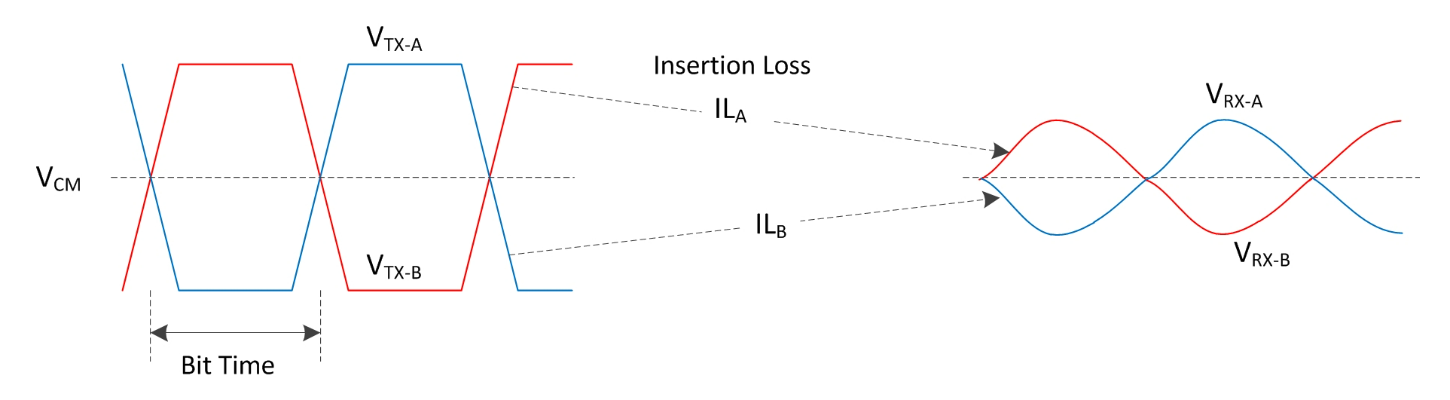
Fig.6 Schematic diagram of signal quality affected by line insertion loss on differential transmission lines

三、The Harm of Common Mode Noise

So, what is the problem with common mode noise? Why is it often necessary to focus on suppressing common mode noise on the circuit in EMC testing? Of course, in order to meet the EMC certification standards of various countries, it is necessary to limit the amplitude of common mode and differential mode signals, achieve product safety, and reduce the potential harm to the power grid or neighboring devices that may be generated by electrical equipment on the power consumption side. Secondly, from the perspective of power integrity and signal integrity, most electrical equipment and appliance controllers operate at low voltage, and additional noise voltage may cause abnormal control signals or transmitted data, even errors and downtime. These abnormal interferences may come from both the circuit board and its noise RF interference, such as mobile device disconnection or broadcast noise whistling. Finally, excessive common mode noise is likely to be emitted into space in the form of high-frequency radiation, such as in larger common mode circuits or on conductors similar to antennas, posing long-term health hazards that are not noticeable to humans.

To simplify the problem, we equivalent the transmission line to a Hertz magnetic couple and obtain the common mode noise radiation model as shown in Fig.7. The distance between the test point and the center position of the common mode transmission line is d, which is generally much larger than the size of the circuit and is therefore a far-field test point. Therefore, for the far-field radiation of the antenna, its field strength is:

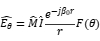
Among them, 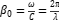 is the phase constant corresponding to the radiation wavelength,  is the spacing between the test positions, 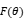 is the plane angle deviated by θ degrees from the antenna radiation pattern, and for Hertz magnetic couples 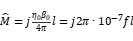,  and 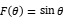, depend on the antenna type. Since the radiation received at the far point is the simultaneous action of two common mode lines at an angle of  , therefore:

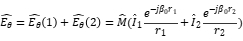
For common mode noise, as shown in Fig.7: 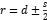 and 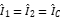, the maximum radiation at the test point is obtained as follows:

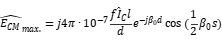
When the line spacing s is small enough 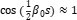 So it can be simplified as:

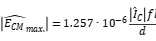
Therefore, the intensity of common mode radiation is proportional to the length of the common mode transmission line and decreases with distance. Give an example of the magnitude of this amplitude: assuming a common mode transmission line length of 1 meter and a common mode current amplitude of 7.96 µA, corresponding to a 3-meter field test as FCC Class B at 30MHz, the radiation intensity is:

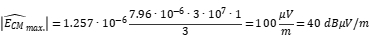
This intensity is exactly the standard limit. If there is a 1-meter conductor or person at the 3-meter test point, it will feel a voltage of 100 µV. Long term exposure to such an environment has a serious impact on human health, and the accumulated radiation may cause various chronic diseases or individual lesions, which is also the important significance of EMC certification.

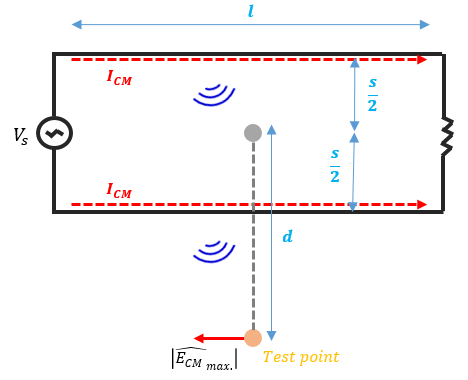
Fig.7 Radiation Model and Test Point Diagram of Common Mode Noise

The waveform structure on most switch circuits can be classified as a trapezoidal wave, and its frequency spectrum shows two stages of deceleration from 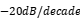 to 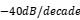 with the increase of harmonic levels. The nodes are the first angular frequency and the rising edge time angular frequency. The frequency spectrum of the radiation intensity of the common mode mentioned above clearly increases with frequency by 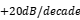. Therefore, for common switching power supplies and square wave signal circuits, the common mode radiation spectrum will roughly show the distribution characteristics of first rising and then falling as shown in Fig.8. Therefore, the middle section is the part that needs special control or suppression.

Fig.8 Distribution of common mode noise radiation intensity corresponding to common trapezoidal waves

四、 Selection of common mode inductors

For power lines, the source of common mode noise is relatively clear, but stray factors are difficult to measure through instruments. In most cases, the results are gradually approximated by analyzing after testing, so accumulated experience is very important. When introducing the application of common mode inductors in Section 2 of this article, it was already mentioned that the theoretical estimation of the amplitude of common mode noise and the corresponding inductance requirements of common mode inductors can serve as a starting point for early experiments.

Usually, the common mode inductor used in the filtering stage of AC-DC power input adopts a closed magnetic circuit magnetic ring as the magnetic core. The advantage of this is that it can easily achieve very low leakage inductance and very high coupling coefficient. For high input voltage and relatively low switching frequency, it can provide good high common mode impedance to suppress high amplitude common mode noise amplitude. Due to the fact that the magnetic permeability of magnetic materials can be divided into inductive parts 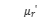 and the loss part  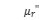When the magnetic core approaches or exceeds the highest impedance characteristic point, the loss part will occupy the main part of the impedance. At this time, noise suppression is no longer achieved by reducing the noise amplitude through inductive impedance, but by absorbing the noise energy through loss heating. Therefore, an appropriate saturation degree (over saturation will cause impedance reduction) will not affect the noise suppression effect,so we do not need to search for saturation current parameters similar to those in power inductors.

When selecting common mode inductors.Meanwhile, if the leakage inductance part, such as a 1mH inductance coupling coefficient of 99%, there will be 10uH leakage inductance present on the differential circuit. When considering differential mode noise suppression (usually LC filter bridge), this part of leakage inductance also needs to be taken into account. Moderate leakage inductance is helpful for suppressing high-frequency differential mode noise, but because common mode inductors mainly use magnetic closed cores, it is easy to cause core saturation at high currents, which has an impact on power conversion efficiency and filtering noise bandwidth. Improving the proportion of leakage inductance can usually be achieved by using square or frame magnetic core structures (UU magnetic core or PQ magnetic core, etc.), or by using asymmetric windings (). The specific selection needs to be determined by the user through differential common mode separator identification testing to determine whether it is necessary.

For the parameters of common mode inductance, they mainly include the single side inductance value, Rdc， Rated current, rated voltage, and withstand voltage Hi pot. The unilateral inductance value mainly determines the size of the common mode impedance. Rdc is the DC loss of the wire, and the temperature rise caused by the loss generates the rated current limit. Finally, because it is used on high-voltage lines, the voltage limit and safety requirements are marked separately. However, users prefer to evaluate the filtering effect, so in general, the specification book will provide two forms of impedance characteristic curves. One is the common mode/differential mode impedance form shown in Fig.9-a, and the other is the insertion loss dB form shown in Fig.9-b. The two are equivalent, and the insertion loss dB form curve is formed by converting the common mode/differential mode impedance into a system with 50 Ω+50 Ω.

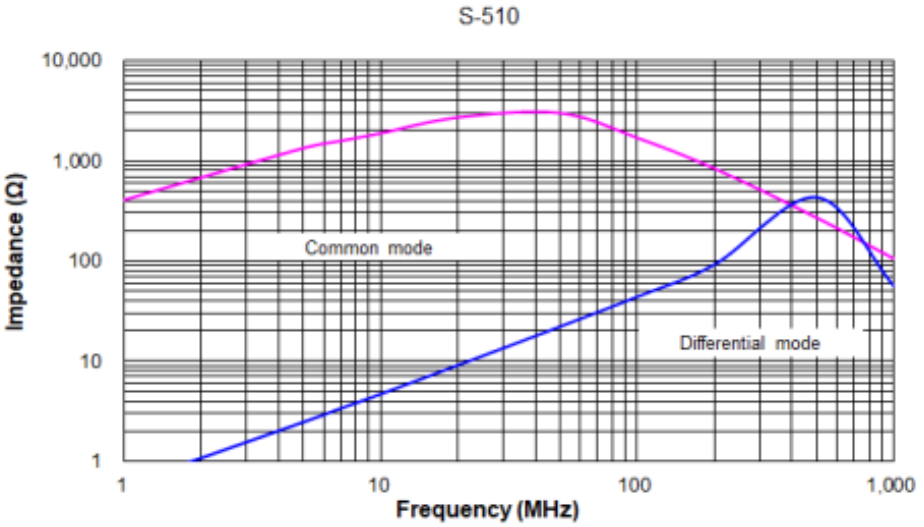
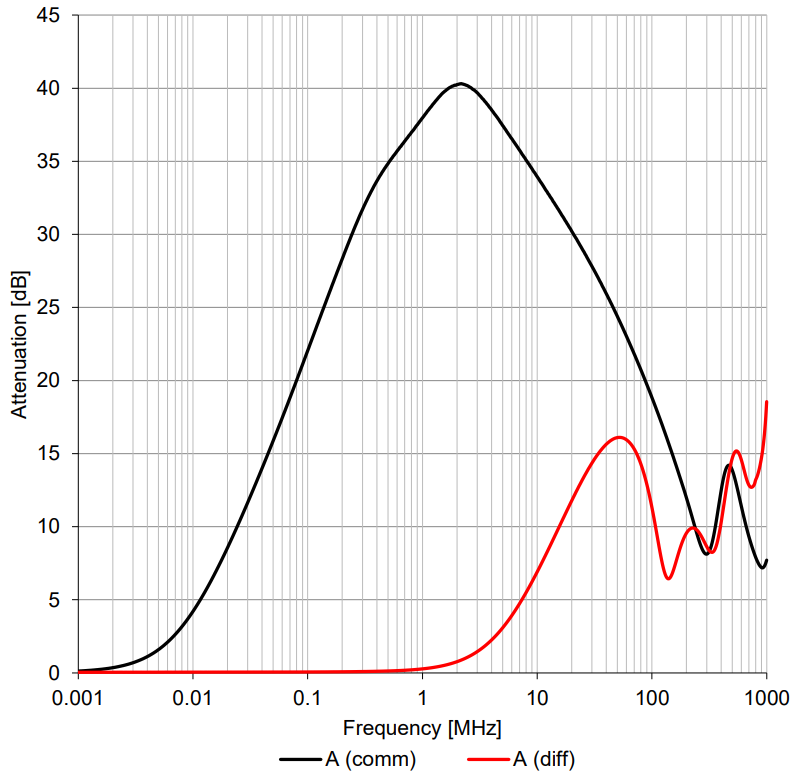
Fig.9 (a) Common mode/differential mode impedance form (b) Insertion loss dB form

For the same common-mode series, packaging structures of different sizes are suitable for different current sizes and filtering bandwidths: the larger the size, the lower the magnetic resistance of the magnetic core, which can reduce the number of winding turns, so that the wire diameter of the copper wire can be enlarged and a larger current loop can be used; the higher the inductance value or the lower the stable frequency of the material's magnetic permeability, the narrower the applicable filtering bandwidth, and such a common-mode inductor placed in the loop is likely to have no noise suppression effect on the high-frequency end.

Codaca Electronics' common mode inductors are currently mainly divided into two parts: signal lines and power lines. There are over 10 series and 50 different sizes of packages, as well as nearly 300 different standard part numbers. They are widely used in signal lines such as CAN BUS, RS485, and different offline power supply devices ranging from a few watts to several kilowatts. Our R&D technology team can also help users from testing to analysis, or customize adaptation specifications, to ultimately completing relevant EMC certifications.

Reference

[1] Infineon Technologies AG. Engineering_report_DEMO_5QSAG_60W1-AN-v01_00-EN.pdf. www.infineon.com

[2]  CODACA Inductor Product Information：www.codaca.com

[3] Clayton R.Paul. Introduction to Electromagnetic Compatibility. 2nd Edition. Wiley-interscience.

[4]  Bhag Singh Guru and Huseyin R. Hiziroglu. Electromagnetic Field Theory Fundamentals. 2nd Edition. Cambridge University Press.

Explanation of Intellectual Property Protection

CODACA "or" Codaca "is a registered trademark of Shenzhen Codaca Electronic Co., Ltd. Any use or reference of text, data, or other types of public information containing intellectual property content published or distributed by Shenzhen Codaca Electronic Co., Ltd. is within the scope of intellectual property protection of Shenzhen Codaca Electronic Co., Ltd. Shenzhen Codaca Electronic Co., Ltd. reserves the relevant intellectual property declaration, rights protection, and other protective rights. To clarify that you do not have any potential intellectual property conflicts in the relevant matters, please contact Shenzhen Kedajia Electronics Co., Ltd. if necessary.